1、 首先,确定函数的定义域,根据函数特征,函数自变量可以取全体实数,即定义域为:(-∞,+∞)。

2、 第一步,确定函数的单调性,通过函数的一阶导数,判断函数的单调性。

3、对y=0.5^(-6x^2+4x+3)两边同时求导,得: dy/dx=0.5^(-6x^2+4x+3)*ln0.5*(-12x+4)=-ln2*0.5^(-6x^2+4x+3)忮氽阝另* (-12x+4),即:dy/dx=ln2*0.5^(-6x^2+4x+3)* (12x-4),令dy/dx=0,则-12x+4=0,即x=1/3,则:(1)当x∈(-∞, 1/3)时,dy/dx<0,此时函数为单调减函数;(2)当x∈(1/3,+∞)时,dy/dx>0,此时函数为单调增函数。
4、 第二步,计算函数的二阶导数,解出函数的拐点,判断函数的凸凹性,即可得到函数的凸凹区间。

5、 观察得到函数的极限,本题主要是在正负无穷大处的极限。则函数y在垓矗梅吒x=1/3时,函数y取得最小值,即:ymin=f(1/3)=0.5^(11/3).

6、 第三步,根据定义域和函数的上述性质,列出函数的五点示意图。
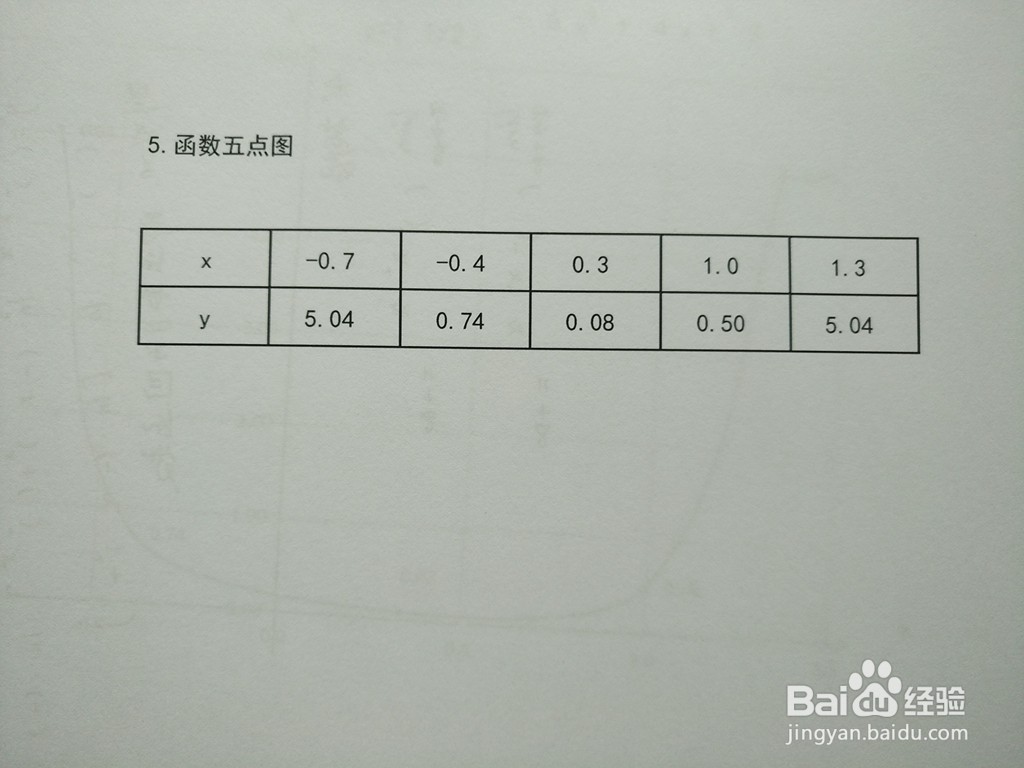
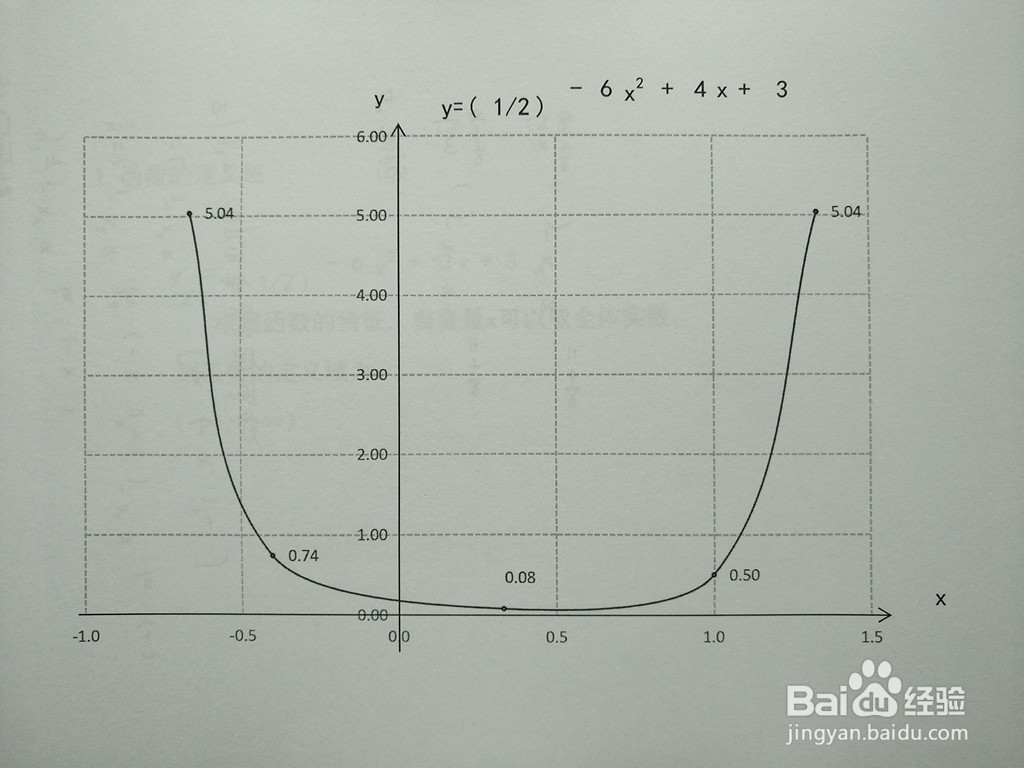
7、 第四步,结合本题函数的定义域、值域、单调性、凸凹性、极限,以及单调和凸凹区间,即可画出函数的示意图。