1、如果y是奇数,左边可以分解为y+2i和y-2i的乘积,我们要证明y+2i和y-2i互素。

2、于是,y+2i必定是某个Gauss整数(设为a+bi)的三次方。
我们要证明,b=-2。
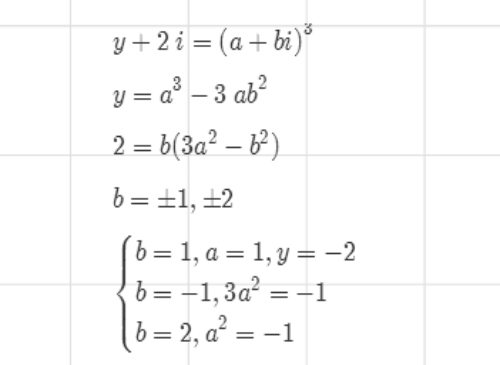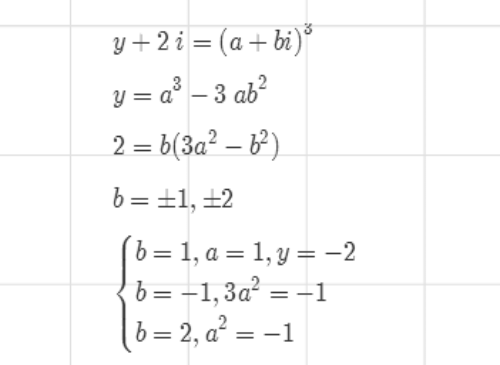
3、根据b=-2,可以找出两组解。
这是y是奇数的时候,仅有的两组解。

4、当y是偶数,那么z也是偶数。设x=2p,y=2q,那么:
4p^2+4=8q^3
p^2+1=2q^3
所以p必定是奇数。
两边在Gauss整数环内部分解因式:
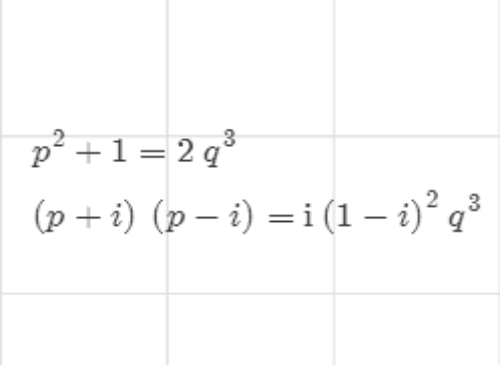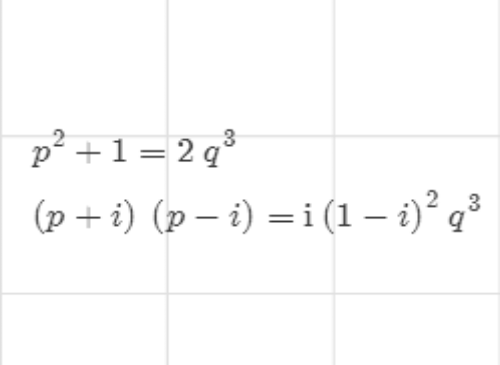
5、假设p+i和p-i的最大公因数是r,那么r可能等于1,1-i,2。
如果r=1,那么,p+i和p-i互素,此时,2只能整除p+i和p-i其中的某一个,这是矛盾的;
r也不可能等于2;
所以,r=1-i。
于是,有下面的分析:
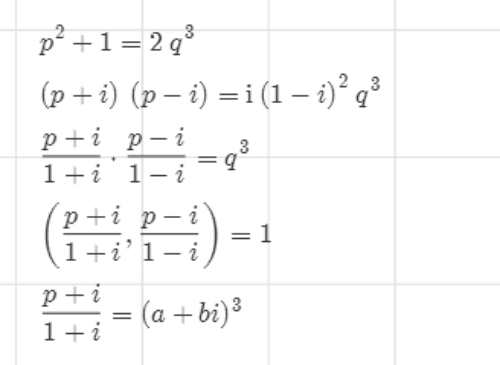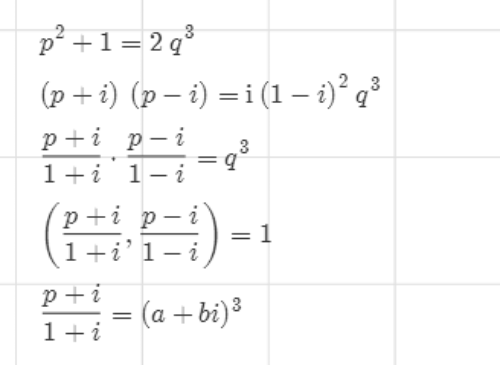
6、分别比较实部和虚部,得到下面两个等式。
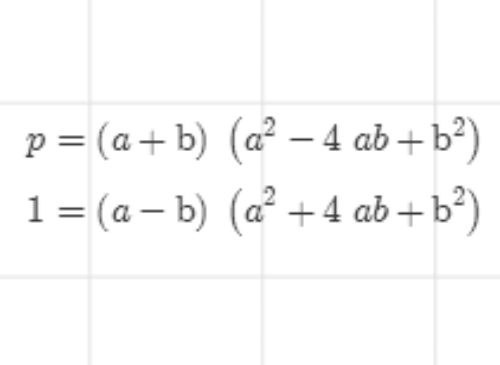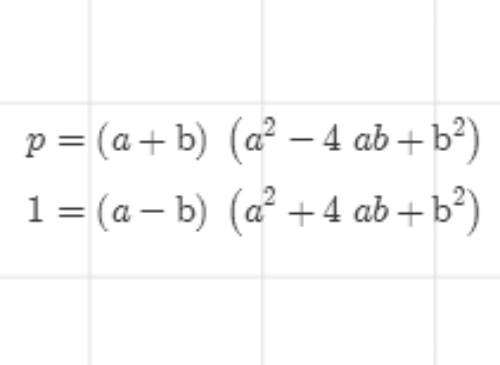
7、根据第二个等式,可以找出满足要求的a和b。

