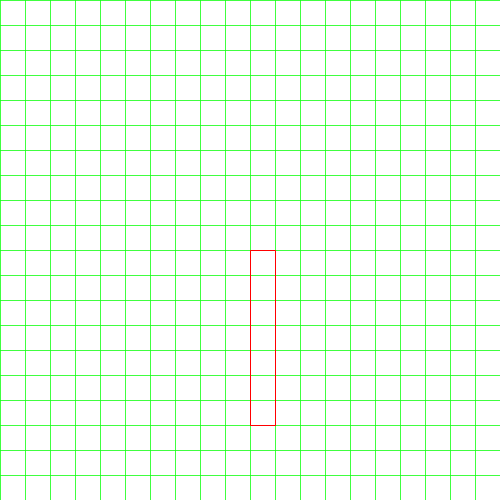
1、我们先写一个自定义函数,用来根据给定的格基绘制相应的格。
f[w_, J_, color_, opacity_]
其中,w代表格子的某个顶点,J是由格基组成的矩阵,color代表格子的颜色,opacity代表透明度。

2、比如,Z^2的一个以原点为顶点的格子可以画为:
Show[f[{0, 0}, {{1, 0}, {0, 1}}, Green, 1], Axes -> True]
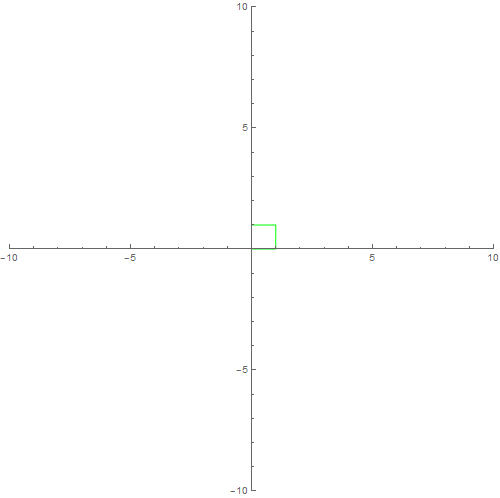
3、我们当然可以把一定范围内所有的格子全部画出来:
A = Tuples[Range[-12, 11], 2];
Show[f[#, {{1, 0}, {0, 1}}, Green, 0.5] & /@ A,Axes -> True]
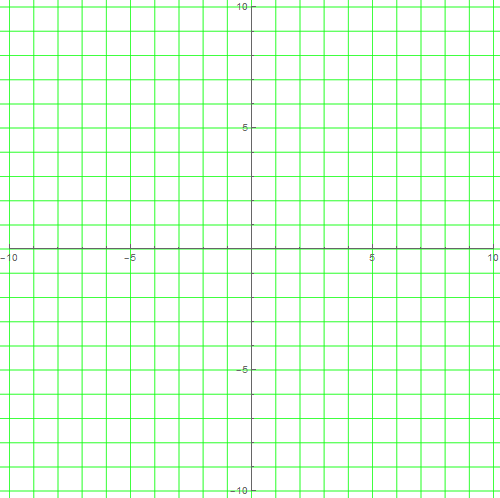
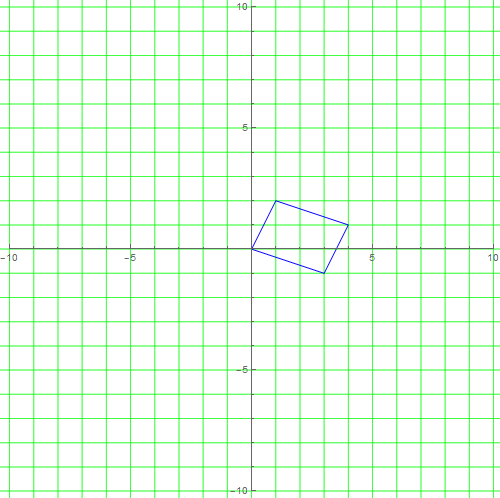
4、用矩阵a左乘,会把格子变成别的形状:
a = {{3, 1}, {-1, 2}};
Show[
f[#, {{1, 0}, {0, 1}}, Green, 0.5] & /@ A,
f[{0, 0}, a, Blue, 1], Axes -> True]
a把一个绿色的小正方形变成了一个蓝色的平行四边形。
注意,这里直接把a当成了格子的基,因为a乘以2*2的单位矩阵,仍等于a。
5、我们也可以把附近所有的蓝色格子全部画出来:
Show[
f[#, {{1, 0}, {0, 1}}, Green, 0.5] & /@ A,
f[#, a, Blue, 1] & /@ (A.a\[Transpose]),
Axes -> True]

6、参考《【抽象代数】Z矩阵的对角化》里面的方法,可以把矩阵a简化为:
b={{1,0},{0,-7}};
那么我们可以画出b对应的格子:
Show[
f[#, {{1, 0}, {0, 1}}, Green, 0.5] & /@ A,
f[{0, 0}, b, Red, 1]]
这是一个长条形的格子,恰好是由7个1*1的格子组成。