求f(x)=lntanx的不定积分:
∫lntanxdx
=x*lntanx-∫xd(lntanx)
=x*lntanx-∫[x*(secx)^2)/tanx]dx
=x*lntanx-∫[x/(sinx*cosx)]dx
=x*lntanx+2*∫[x/sin(2x)]dx
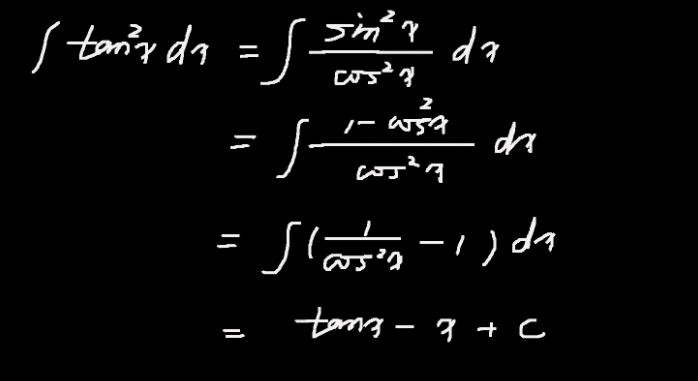
解释
根据牛顿-莱布尼茨公式,许多函数的定积分的计算就可以简便地通过求不定积分来进行。这里要注意不定积分与定积分之间的关系:定积分是一个数,而不定积分是一个表达式,它们仅仅是数学上有一个计算关系。一个函数,可以存在不定积分,而不存在定积分,也可以存在定积分,而没有不定积分。
