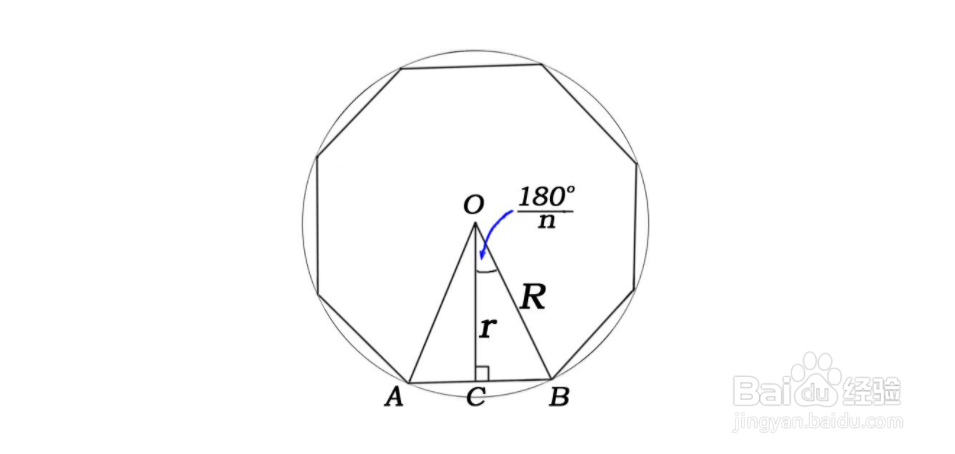
1、已知正多边形中心的情况下,边心距可通过从正多边形中心向某一边作垂线段;或连接正多边形中心和某一边的中点求得。
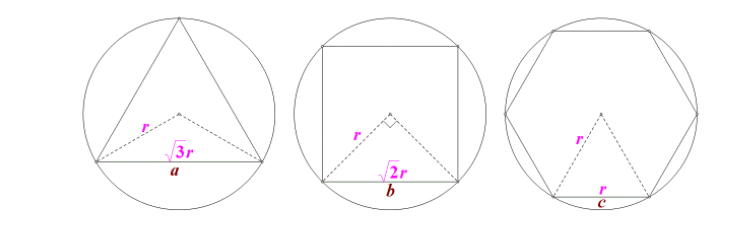
2、不知中心的情况下,可以根据垂径定理,通过两条边的垂直平分线的交点来确定正多边形的中心,然后求出边心距。
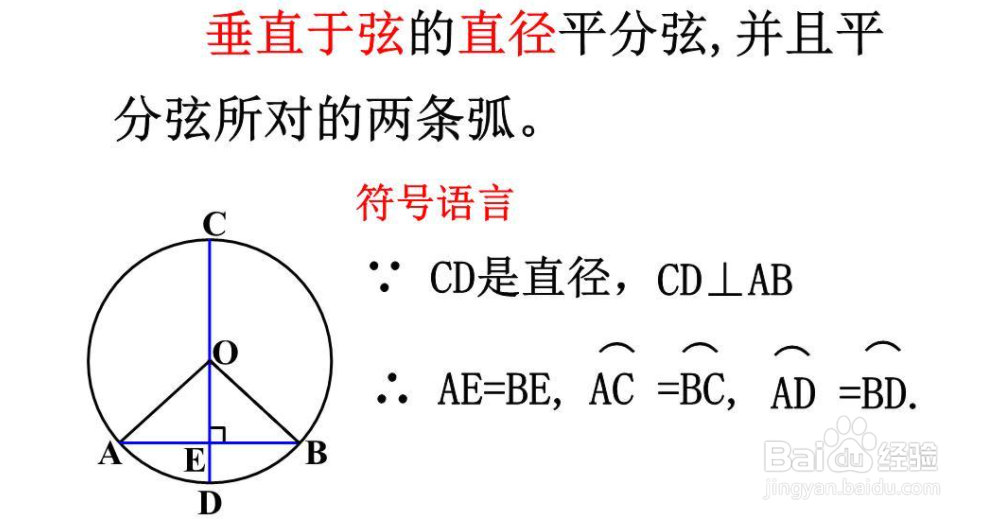
垂径定理是数学平面几何(圆)中的一个定理,它的通俗的表达是:垂直于弦的直径平分弦且平分这条弦所对的两条弧。数学表达为:如概述图,直径DC垂直于弦AB,则AE=EB,弧AD等于弧BD(包括优弧与劣弧),半圆CAD=半圆CBD。
3、边心距可以通过正多边形外接圆的半径和边长求出,如果正n边形的外切圆的半径为R边长为s,则边心距为:
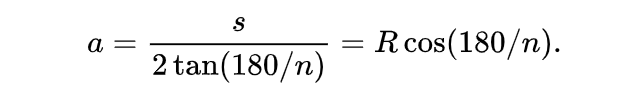
4、正多边形求边心距的方法是:
做其中两边的垂直平分线,得其交点是圆心。将各端点同圆心连起来,这就是半径R。正N多边形就有N条半径,每两条半径之间的夹角就是360/N。边长就是2Rsin(180/N),边心距就是Rcos(180/N)。周长就是2NRsin(180/N),面积就是NRsin(180/N)Rcos(180/N)。