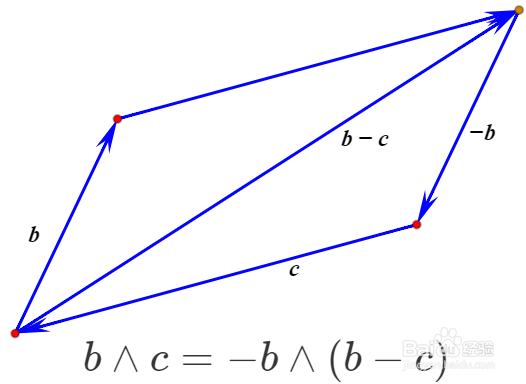
1、给定两个向量a和b,那么a∧b表示的是它们形成的平行四边形的有向面积。
设c=-(a+b),那么a、b、c可以围成三角形,a∧b还可以表示这个三角形的有向面积的二倍。
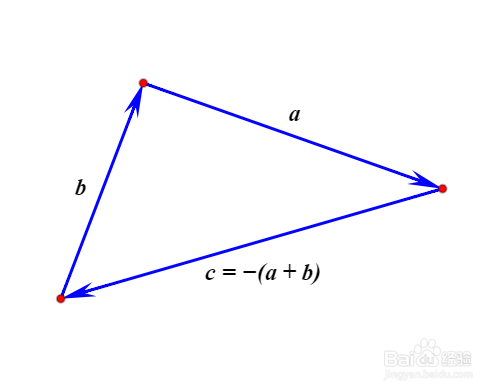
2、同样的,b∧c也是这个三角形的有向面积,且与a∧b的方向相同(同为顺时针)。
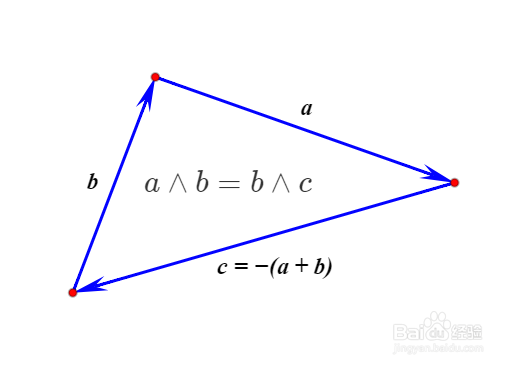
3、于是,b∧c=a∧b。
注意,这时候我们还不知道反交换律是否成立,但是我们知道结合律是成立的。
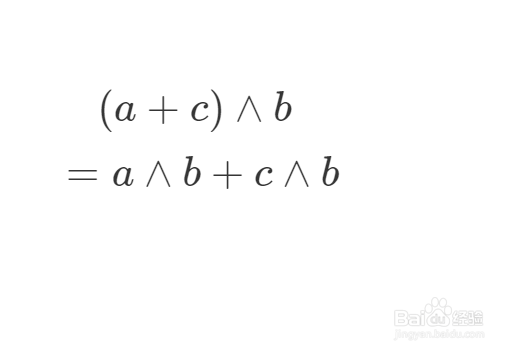
4、所以就有如下的推理过程,最终证明了外积满足反交换律。
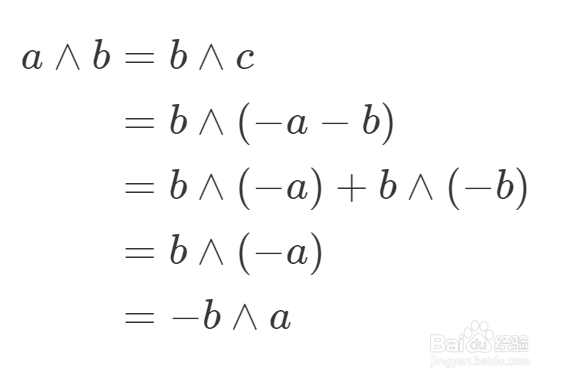
5、上面过程中,用到一个结论:
b∧b=0
这是因为单独一个向量,不可能张开一个平行四边形。
我们可以认为这是一个面积为0的平行四边形,已经与方向无关了。
实际上,这一点与反交换律是相辅相成的:
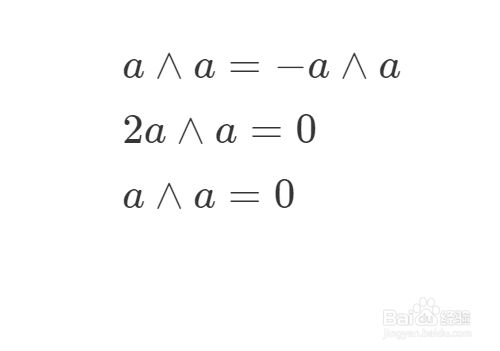
6、观察图片,给出下图的证明。
这其实是一个无言的证明,只需要你会分辨逆时针方向和顺时针方向。