1、首先要确定定义:对于任意给定的正数ε(无论它多么小),总存在正数δ ,使得当x满足不等式0<|x-x。|<δ 时,对应的函数值f(x)都满足不等式: |f(x)-A|<ε ,那么常数A就叫做函数f(x)当 x→x。时的极限。
下图有具体的定义
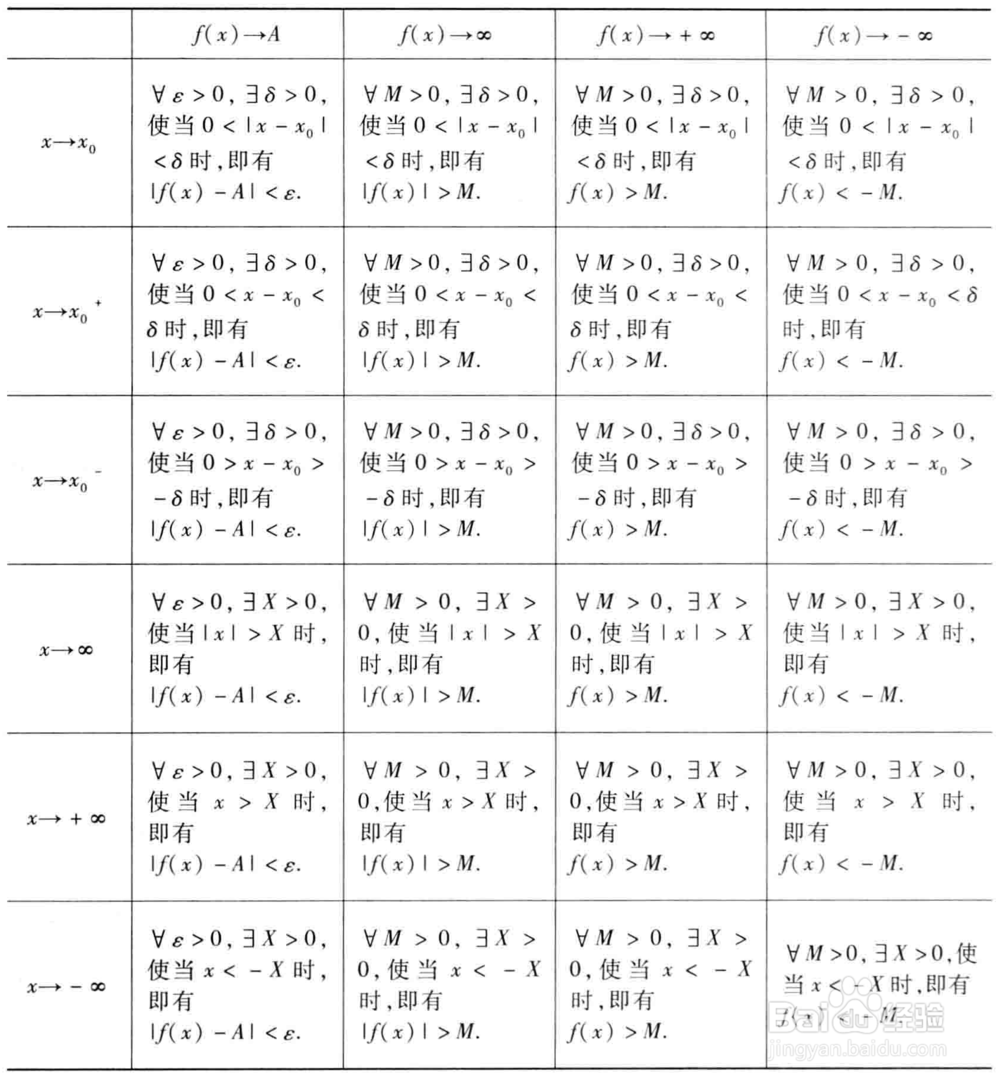
2、确认了定义,其次就要根定义求函数的极限;题目:证明limx趋向于无穷1+x^3/2x^3=1/2

3、然后就需要解题,千万记住定义。 因为|{(1+x^3)/2x^3}-1/2|=1/2|x|^3,要使|{(1+x^3)/2x^3}-1/2|<ε, 只要1/2|x|^3<ε,即|x|>1/3√2ε, 所以任意ε> 0,取 X =1/3√2,则 当x>X,就有|{(1+x^3)/2x^3}-1/2|<ε,故limx趋向于无穷1+x^3/2x^3=1/2

