1、函数中含有根式,即可得到关于自变量的不等式,进而解析函数y=x+√(5+x)的定义域,且定义域为半开半闭区间。

2、定义域是指该函数的有效范围,函数的定义域就是使得这个函数关系式有意义的实数的全体构成的集合。
3、计算函数y=x+√(5+x)的一阶导数,根据一阶导数的符号,即可判断函数的单调性,为增函数。
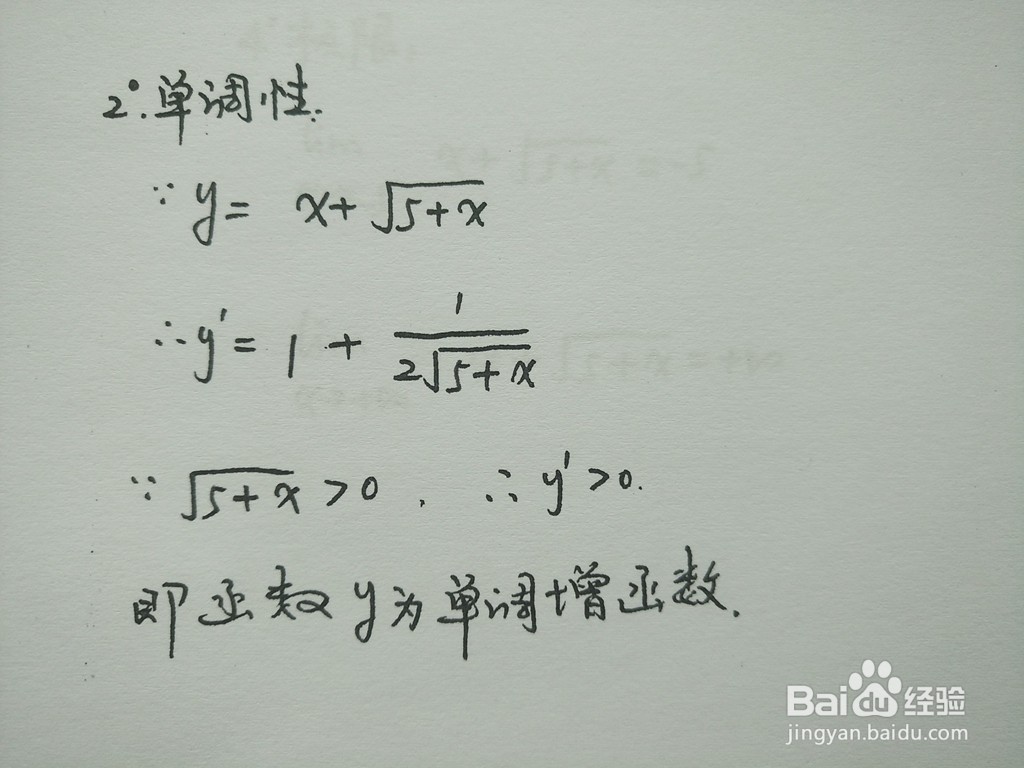
4、函数的凸凹性是函数图形的一种特性。对于一个函数f(x),如果在某区间上,其函数图形是向下(或向上)凸出的,那么我们就说这个函数在这个区间上是凹函数(或凸函数)。

5、计算函数y=x+√(5+x)的极限,主要判断函数y=x+√(5+x)在无穷远处等处的极限。

