证明：
如果AB=0，那么B的每个列都是齐次方程组AX=0的解。
设r（A）=r，那么方程组AX=0最多有n-r个线性无关的解，
所以：r（B）<=n-r=n-r(A)。
因此，r（A）+r（B）<=n。
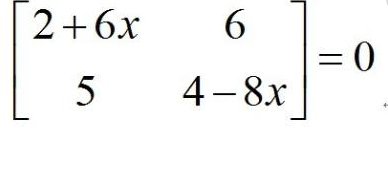
扩展资料：
矩阵运算在科学计算中非常重要 ，而矩阵的基本运算包括矩阵的转置，共轭和共轭转置等。
①转置：
把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵 ，这一过程称为矩阵的转置
矩阵的转置满足以下运算律：
②共轭：
矩阵的共轭定义为:
。一个2×2复数矩阵的共轭如下所示 ：
则
③共轭转置：
矩阵的共轭转置定义为：
，也可以写为：
。一个2×2复数矩阵的共轭如下所示：
则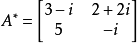
参考资料：百度百科-矩阵（数学术语）
